Why Every Baseball Game Breaks the Rules
If you’re a baseball fan, you already know a few things about the baseball diamond — bases are 90 feet apart, for example. That’s in the rulebook (pdf). You’ll see it, clear as day, in rule 2.01: “The infield shall be a 90-foot square.” Appendix 1 of the rule book has some nice images, too — it shows 90-degree angles at first, second, third, and home, and 90-foot lines connecting those four points.
What you may not know is that the rule book also tells us how big home plate has to be — and it’s pretty specific. That’s in rule 1.05 if you want to look it up, but here’s the relevant text:
[Home plate] shall be a 17-inch square with two of the corners removed so that one edge is 17 inches long, two adjacent sides are 8 1/2 inches and the remaining two sides are 12 inches and set at an angle to make a point. It shall be set in the ground with the point at the intersection of the lines extending from home base to first base and to third base; with the 17-inch edge facing the pitcher’s plate, and the two 12-inch edges coinciding with the first and third base lines.
And just to clear up any ambiguity, the images in Appendix 1 of the rules make it clear that those 12-inch edges are part of the 90-foot distance from home to first and third bases, respectively.
What Rule 1.05 doesn’t spell out exactly is that “two sides are 12 inches and set at an angle to make a point” have to be set at a 90-degree angle (a “right angle,” in math parlance) in order for the field to be a square and meet the requirements of the other rules. But that point is, in fact, supposed to be right angle. Just look at the following diagram, also found in the rulebook:
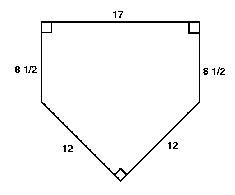
See those little squares drawn inside the angles? If you think back to your high school geometry days, you’ll remember that those mean that the angle is a right angle. And if you dig into your memories a bit more, you’ll probably remember your geometry teacher telling you about something called the Pythagorean Theorem. (For those readers who are big baseball fans, I’m not talking about the theorem of the same name which is used to estimate how many wins and losses a team should have based on their runs scored and runs allowed.) It applies to right triangles — that is, triangles with a right angle. The squares of the hypotenuse (the side across from the 90-degree angle) is equal to the squares of other two sides added together. Or, in formula form:
a2 + b2 = c2
Where a and b are the lengths of the shorter sides (the “legs”) and c is the length of the hypotenuse.
Home plate isn’t a triangle — it’s a pentagon — but it still follows similar principles. It’s pretty easy to say why: if you remove the two 8.5-inch sides from home plate and bring the top edge down you’ll end up with what, per the image, is a right triangle — two sides of 12 inches that meet at a 90-degree angle and a 17-inch hypotenuse.
And that’s a problem. Math-wise, that is.
Take 12 and square it and you’ll end up with 144. Square the other 12 and you get another 144; add those up — a2 + b2 — and you’re at 288. But if you take 17 and square that? It’s 289. The math is close, but not quite right.
It’s an almost imperceptibly small problem, but it means that if the top edge of home plate runs 17 inches, the angle at the point of home plate is a bit larger than 90 degrees. And in turn, this means that, despite rule 2.01’s insistence, the infield cannot quite be a square. In theory, the visiting manager could go to home plate, armed with a ruler and protractor, and demonstrate that the home team is violating the rules. In practice, we’ve never seen that happen, and thankfully so: we don’t know what the remedy would be, but it’d be really hard to fix.
Bonus fact: The baseball rules are oddly specific in other ways. For example, pitchers can’t use foreign substances to “intentionally discolor or damage the ball” pursuant to rule 3.01. The rule specifically references a few such substances — soil, sandpaper, emery paper, and… licorice. It’s not as absurd as it sounds — black licorice was once commonly used to mark up a ball, rendering it harder to see and therefore, harder to hit.
From the Archives: One Spud, You’re Out: How a trick play ended up getting the catcher out.
Related: A really great baseball cap.
