Spam Economics

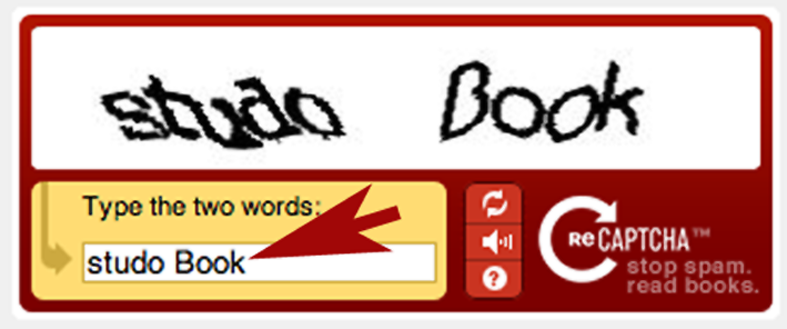
Pictured above is something called a CAPTCHA — a “Completely Automated Public Turing test to tell Computers and Humans Apart.”  CAPTCHAs are used to allow real people into certain areas of websites — comment sections on blogs, for example — and to keep automated services, like spammers, away. With probably millions of blogs, forums, etc. around the Web, the CAPTCHA is probably the best method we have at keeping feedback from being overwhelmed with links to sites which claim to cure baldness and other (typically more insidious) such things.

But of course, some of the spammers have found a way past the CAPTCHA. When computers can’t get through, they turn to people.

The criteria for a CAPTCHA, per a team of U.C. San Diego researchers investigating how spammers weave their way though the gates (pdf here), is three-fold. First, the problem needs to be easily solved by people; after all, you want people to be able to leave their comments or thoughts. Second, the test has to be “easily generated and evaluated,” and practically speaking, by some sort of computer algorithm and database. This makes sense, as the number of, say, forum posts could easily overwhelm the forum owner if he or she had to create and/or evaluate each test by hand. Finally, the CAPTCHA cannot be easily solved by a computer, as the entire point is to weed out automated replies. (And the trick is not just to get readers to click. Because Google’s search engine treats links to a page as a “vote” for that page’s value, having a lot of links to your website may have a positive effect on your website’s rank in the search results.) 

The work-around, per the researchers, is something they call “paid solving.” They came across a blog post written in 2006 by an employee of computer security company Symantec, discussing an ad placed on a freelancer-finding job board. The advertiser was looking for someone to solve CAPTCHAs over a 50-hour workweek, and received 58 bids ranging between $30 and $1,000 within the first week. (The site canceled the advertisement thereafter.) The Symantec employee assumed that in 50 hours, someone could solve about 6,000 CAPTCHAs (at 30 seconds per puzzle), making the low-end bid come out to under two cents each.

Four years later, the New York Times delved deeper. A report from Mumbai, India noted that high-end spamming companies (yes, they exist) hired cheap laborers in India, Bangladesh, China, and in other developing nations where such labor is readily accessible. Those workers are asked to solve the cryptic-looking text, and, once through the door, sign up for accounts, post messages, or, as the Times so aptly phrases, “carry out other mischief.” For their trouble? Some students working on CAPTCHA-busting “typically work two and a half to three hours a day from their homes and make at least $6 every 15 days,” which sounds terrible, but isn’t bad relative to other wages; the Times further notes that “[u]nskilled male farm workers earn about $2 a day in many parts of India.”

While spammers may find these nickels and dimes well-spent on finding a solution, the advent of “paid solving” doesn’t bother Google, which makes some of the leading anti-spam/CAPTCHA software. As one engineer told the Times, “[o]ur goal is to make mass account creation less attractive to spammers, and the fact that spammers have to pay people to solve captchas proves that the tool is working.”.

Bonus fact: You may notice at the bottom right of the image above that the logo reads “stop spam. read books.” That particular anti-spam service, called reCAPTCHA (and now owned by Google), doesn’t just keep the spammers away. One of the words shown is used for that purpose, but the other isn’t. As reCAPTCHA explains, “reCAPTCHA improves the process of digitizing books by sending words that cannot be read by computers to the Web in the form of CAPTCHAs for humans to decipher. More specifically, each word that cannot be read correctly by OCR [“Optical Character Recognition”] is placed on an image and used as a CAPTCHA.” With literally millions of reCAPTCHA attempts happening each day, the service is helping digitized old texts. (And at $6 every 15 days, spammers are helping, too.)

From the Archives: From Sheep to Books: Why are books the size and shape they are?

Related: Spam.